| E0313 |
LA FLEUR D'ULYSSE.
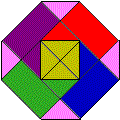 Le carré central a une aire de 1 cm², or il est partagé en quatre triangles rectangles isocèles. Le carré central a une aire de 1 cm², or il est partagé en quatre triangles rectangles isocèles.
Le carré dont les côtés ont pour milieu un sommet de ce carré central a donc pour aire 2 cm².
Si on groupe par 2 les rectangles qui apparaissent sur le bord de l'octogone, on obtient encore 4 cm².
Enfin les 4 triangles rectangles isocèles permettent de reconstituer le carré central donc la somme des aires de ces 4 triangles égale 1 cm².
Au total, l'octogone a donc une aire de 7 cm².
Les grands élèves de collège pourront éviter ce dénombrement de triangles isocèles. Si on ajoute à cette fleur 4 triangles rectangles isocèles ( tels que les triangles violets, d'aire 1/4), on obtient un grand carré de côté 2 v2 . |
| E0314 |
LE HANGAR DE PAULINE.

Pauline, la champenoise, vient de m'envoyer deux jolis dessins, celui de son hangar et celui du hangar de Marina.
Appelons un 1-bâtiment le hangar de Pauline : il a 15 arêtes.
Dessinez un 2-bâtiment : vous trouverez vite qu'il a 21 arêtes.
Avec un 3-bâtiment, vous trouverez 27 arêtes.
Avec un 4-bâtiment, vous trouverez 33 arêtes.
Et celui de Marina est formé de cinq bâtiments et comporte trente-neuf arêtes.
On observe maintenant que pour chaque bâtiment supplémentaire, il faut ajouter 6 arêtes.
Donc un 1-bâtiment a 15 arêtes, un 2-bâtiment a 15 + 6 arêtes, un 3-bâtiment a 15 + 6 ´ 2 arêtes,
un 4-bâtiment a 15 + 6 ´ 3 arêtes, un 5-bâtiment a 15 + 6 ´ 4 arêtes,… et un 10-bâtiment comme celui d'Olivier a 15 + 6 ´ 9 arêtes, soit 15 + 54 = 69 arêtes
Le hangar d'Olivier est formé de 69 arêtes
Remarque : Il est maintenant facile d'écrire la formule qui permet de calculer rapidement le nombre d'arêtes d'un hangar formé de n bâtiments : un n-bâtiment possède 15 + 6 ´ ( n-1 ) arêtes. |
E0315
|
LE LIVRE DE JEANINE.

Il est, ce lundi, grand ouvert. Tiens dit-elle en regardant les deux numéros de page visibles, si j'additionne ces deux nombres, j'obtiens 49.
Mardi, Jeanine notre lectrice ouvre de nouveau son livre. Tiens dit-elle en regardant les deux numéros de pages visibles, si je calcule le produit de ces deux nombres, j'obtiens 600.
Pour le lundi, il faut, bien entendu, trouver deux nombres entiers consécutifs dont la somme est 49. Ce ne peuvent être que les pages 24 et 25.
Pour le mardi, il faut trouver 2 nombres entiers consécutifs dont le produit est 600.
Après quelques essais, on trouve vite que ce sont les pages 24 et 25.
|
| E0316 |
LE CADEAU DE CATHERINE.
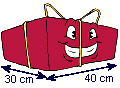 Pour sa première fête des mères, Catherine a reçu un bien joli cadeau. Pour sa première fête des mères, Catherine a reçu un bien joli cadeau.
Une ficelle de 2.70 m suffit pour le fermer (attention, le dessin n'est pas fait à l'échelle).
Catherine a utilisé 30 cm de ficelle pour le noeud .
Appelons (en cm) L la longueur, l la largeur et h la hauteur de ce paquet.
Alors 2L + 2l + 4h = 270 – 30
Donc 80 + 60 + 4h = 240 alors 4h = 100 et on obtient h = 25.
La 3ème dimension du cadeau est 25 cm |
| E0317 |
LA STAR DE CONTY.
 Observez bien cette étoile à 6 branches. Par un découpage assez simple on s'aperçoit qu'elle est formée de triangles équilatéraux. Observez bien cette étoile à 6 branches. Par un découpage assez simple on s'aperçoit qu'elle est formée de triangles équilatéraux.
Nous avons déjà eu ce genre de comptage à faire et nous allons encore procéder en prenant comme unité d'aire un triangle équilatéral élémentaire.
Comptons les triangles équilatéraux formés d' un seul triangle équilatéral : il y en a 12.
Et maintenant les triangles formés de 2 triangles élémentaires, évidemment il n'y en a aucun !
De même avec 3 triangles élémentaires. Par contre avec 4 triangles élémentaires, il y en a 6 exactement en faisant bien attention de ne pas compter un tel triangle 2 fois !
Et pour finir, les triangles formés de neuf triangles élémentaires : on en compte 2.
Au total, il y a donc 20 triangles équilatéraux . |
| E0318 |
LA SUPERSTAR DE VOTRE REVUE ( T 55 )
 Cette splendide étoile magique (il s'agit bien de celle du texte T55) compte 12 étoiles magiques construites avec 12 nombres différents. Cette splendide étoile magique (il s'agit bien de celle du texte T55) compte 12 étoiles magiques construites avec 12 nombres différents.
Mais je n'ai pas dit «construite avec144 nombres ». En effet certaines écritures sont répétées !
Quels sont les deux nombres écrits le plus souvent ?
Observez bien cette étoile d'étoiles magiques et voyez sa construction : l' étoile du haut a permis de construire les onze autres par multiplications et en respectant un positionnement copié sur les nombres de la première étoile. Ainsi, les nombres apparaissant le plus souvent sont ceux qui, sans être trop grands, ont le plus de diviseurs : 12 et 24 ont 6 diviseurs inférieurs ou égaux à 12 ; ils apparaissent donc dans 6 étoiles !
Parmi les nombres carrés, quel est celui qui apparaît le plus souvent ?
Les premiers nombres carrés sont : 0 ; 1 ; 4 ; 9 ; 16 ; 25 ; 36 ; 49 ; 64 ; 81 ; 100 ; 121 ; 144.
Evidement 0 ne figure jamais dans l'étoile d'étoiles ! 1 et 144 n'y figurent qu'une seule fois. Parmi la liste restante des nombres carrés, celui qui peut apparaître le plus souvent est celui qui a le plus de diviseurs sans pour autant être trop grand ! Or 36 est divisible par 1, par 2, par 3, par 4, par 6, par 9, par12, par 18et par 36.
Mais l'étoile de sommet 2 ne peut pas contenir 36 ( 2 × 12 = 24) et l'étoile de sommet 18 n'existe pas . Par conséquent 36 apparaît dans les étoiles de sommet 3, 4, 6, 9 et 12 ; il apparaît donc 5 fois !
36 est le nombre carré qui apparaît le plus souvent.
|
| C0313 |
LE LIVRE DE JEAN 
Il est, ce mercredi, grand ouvert. Tiens ! dit-il en regardant les deux numéros de pages visibles. Le plus petit de ces nombres est le plus petit nombre entier qui est à la fois un carré et un cube (il n'y a pas de page numérotée 0, et nous excluons la réponse triviale: 1)
Quel est ce nombre ?
Le plus simple est peut-être de construire le tableau des carrés et des cubes des nombres entiers à partir de 1 :
Nombre entier x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Carré de x : x 2 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
121 |
144 |
169 |
196 |
225 |
Cube de x : x 3 |
1 |
8 |
27 |
64 |
125 |
216 |
343 |
512 |
729 |
1000 |
1331 |
1728 |
2197 |
2744 |
3375 |
Le plus petit nombre entier qui est à la fois un carré et un cube est 64. |
| C0314 |
LE BOUCHER DE MON VOISIN EST-IL LE VOISIN DE MON BOUCHER ?
 Peut être; regardons y de plus près. Peut être; regardons y de plus près.
Si ces trois personnes habitent le long d'une rue, deux cas sont à distinguer:
- je suis situé entre mon voisin et mon boucher. Alors certainement l'affirmation proposée est fausse.
- sinon, je suis à une extrémité de cette chaîne de trois personnes, et mon voisin et mon boucher sont bien côte à côte. L'affirmation proposée est vraie.
Nous pouvons aussi avoir le cas où ces trois personnes habitent des maisons situées par exemple chacune sur un côté d'un espace triangulaire. Et dans ce cas l'affirmation proposée est vraie.
Quel est ce mystérieux nombre. Il se calcule aisément. En effet
13 × ((( 1 + 1) × 2 ) 2 + (( 1 × 2) + 1) 2 ) = 13 × (( 2 × 2) 2 + ( 2 + 1) 2 ) = 13 × (4 2 + 3 2 ) =
13 × (16 + 9) = 13 × 25 = 325.
Et nous avons ici une combinatoire bien simple.
Je note d(n) le double de n (exemple d (17) = 34 ) et je note s (n) le suivant de n (exemple s (8) = 9). Je peux aussi évoquer le double du suivant d'un nombre n, qui s'écrit d (s (n)) ou plus simplement ds(n). Je peux aussi vous parler du nombre sd (9) qui est 19, nombre que je ne confonds pas avec le nombre ds(9) qui est 20. Calculez donc sds(7) .
Appelons de même c (n) le carré de n.
Le texte propose 6 calculs et dans chacun, j'effectue, dans un certain ordre les trois transformations notées: d, s, c ce qui me donne en fait 6 mots, chacun composé de 3 lettres différentes écrites dans un ordre différent.
325 est impair, ce qui me permet d'éliminer trois transformations ou « mots » qui ne donneraient que des nombres pairs. Ce sont dcs, dsc, cds. Reste 3 mots.
Pour être très très simple, je me contenterai pour chacun des nombres de 1 à 9 (le nombre inconnu a un seul chiffre) de rechercher son « transformé » par chacune des 3 transformations qui me donneront un nombre impair, et je commence ce tableau que vous terminerez :
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
csd |
9 |
25 |
49 |
81 |
121 |
169 |
225 |
289 |
361 |
scd |
5 |
17 |
37 |
|
|
|
|
|
325 |
sdc |
3 |
9 |
|
|
|
|
|
|
163 |
325 apparaît une fois et une fois seulement dans mon tableau. Voilà, le nombre demandé est 9.
(cet exercice conduit assez naturellement l'auteur de ce petit problème à écrire un nouveau texte que vous trouverez dans votre revue « Les héritiers d'Archimède ». C'est le texte T...). |
| C0315 |
LE MANEGE DE RENEE L'INCORRIGIBLE.

Bien fière sur son grand cheval, Renée l'incorrigible compte, compte, compte.
Voilà qui est bizarre: Je compte les gamins qui sont devant moi et je calcule le tiers de ce nombre; puis je compte le nombre de gamins derrière moi et je calcule les trois quarts de ce nombre. En additionnant ces deux nouveaux nombres, je trouve alors... exactement le nombre de passagers de ce manège qui est de....
Combien y a t-il de passagers dans ce manège ?
Appelons x le nombre de gamins, Renée a donc x gamins devant elle mais aussi x gamins derrière elle.
Avec Renée il y a donc x + 1 passagers dans ce manège, On obtient donc l'égalité : x/3 + 3x/4 = x + 1 d'où 4x/12 + 9x/12 = x + 1 alors 13x/12 = x + 1,
donc 13 x -12 x = 12 et x = 12.
Il y a donc 12 + 1 soit 13 passagers dans ce manège.
|
| C0316 |
LE HANGAR DE CHRISTOPHE

Ces constructions sont basées sur le même principe que celui des constructions de Pauline, Marina et Olivier vues dans l'exercice E 0314.
Christophe d'après son dessin va commander 2004 poutres métalliques bien choisies, ce qui semble d'après lui correspondre au nombre d'arêtes qu'il a évalué.
Quel est le nombre maximal de bâtiments du gigantesque hangar de Christophe ? Rappelons la formule vue en remarque dans la solution du problème E 0314 :
un n-bâtiment possède 15 + 6 ´ ( n-1 ) arêtes.
Nous allons donc calculer n-1.
Si 15 + ( n-1) × 6 = 2004 alors ( n-1 ) × 6 = 2004 – 15 = 1989 et n-1 = 1989 : 6 = 331 et il reste 3.
n-1 étant égal à 331 alors n = 332.
Le gigantesque hangar de Christophe est formé de 332 bâtiments
Combien lui restera-t-il de poutres métalliques ?
Christophe a commandé 3 poutres métalliques en trop. |
| C0317 |
TRIANGLES ET PRODUITS
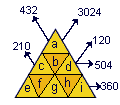 On dispose les neuf entiers de 1 à 9 dans les cases triangulaires et on effectue les produits des nombres d'une même bande dans les trois directions comme indiqué sur la figure. On dispose les neuf entiers de 1 à 9 dans les cases triangulaires et on effectue les produits des nombres d'une même bande dans les trois directions comme indiqué sur la figure.
120 = 3 x 5 x 8
210 = 7 x 6 x 5
360 = 6 x 5 x 4 x 3 x 1
On peut déjà en déduire en observant les intersections des bandes que g = 5, que h = 3 et que f = 6. En conséquence : d = 8 et c = 7 .
D'autre part, 504 = 7 x 8 x 9 et donc b = 9.
432 = 9 x 8 x 3 x 2 x 1 et donc i = 1 et a = 2.
Enfin, 3024 = 2 x 9 x 7 x 6 x 4 et donc e = 4.
En résumé, a = 2, b = 9, c = 7, d = 8, e = 4, f = 6, g = 5, h= 3 et i = 1
|
| C0318 |
SPLENDIDE CARRE
|
a |
b |
c |
d |
e |
f |
a |
4 |
2 |
8 |
5 |
7 |
1 |
g |
2 |
8 |
5 |
7 |
1 |
4 |
h |
8 |
5 |
7 |
1 |
4 |
2 |
i |
5 |
7 |
1 |
4 |
2 |
8 |
j |
7 |
1 |
4 |
2 |
8 |
5 |
k |
1 |
4 |
2 |
8 |
5 |
7 |
|
a = 3 k et b = 2 k et c = 6 k et d = 4 k et e = 5 k et f = d / 4.
Puisque c = 6k et que tous ces nombres utilisent 6 chiffres ( il n ' y a donc pas de retenue) k a pour chiffre des centaines de mille 1 et a se termine donc par un 1 or a = 3k donc k se termine par le chiffre 7 car 7 ´ 3 = 21 ( seul multiple de 3 se terminant par 1).
|
b se termine par le chiffre 4 car b = 2k et 7 x 2 = 14.
c se termine par le chiffre 2 car c = 6k et 7 x 6 = 42.
d se termine par le chiffre 8 car d = 4k et 7 x 4 = 28.
e se termine par le chiffre 5 car e = 5k et 7 x 5 = 35.
Le nombre k est donc 142 857. Ensuite c'est très simple : a = 3 x 142 857 = 428 571 ; b = 2 x 142 857 = 285 714
c = 6 x 142 857 = 857 142 ; d = 4 x 142 857 = 571 428 ; e = 5 x 142 857 = 714 285 et on lit f = 142 8571
Le plus grand nombre de six chiffres é crit dans ce tableau est donc : 857 142
|



