| E0401 |
HUIT NOMBRES CONSECUTIFS…
Il y a certainement plusieurs façons de trouver la réponse et de vous l’expliquer.
On peut en effet calculer de proche en proche ces nombres si on se donne par exemple le premier. Le suivant, c’est ce premier augmenté de 1, le suivant, le premier augmenté de 2,… le dernier, c’est donc le premier augmenté de 7.
La somme de ces huit nombres (qui est 2004) vaut donc 8 fois ce premier augmenté de
1 + 2 + 3 + … + 7 (tiens ! un nombre triangulaire qui est 28), … Et huit fois ce premier nombre, c’est donc la différence 2004 – 28, c'est-à-dire 1976.
Divisons-la par 8 ; on obtient ce premier nombre 247 qui est la réponse demandée.
|
| E0402 |
QUI SUIS-JE ?
Hermès chez les Grecs (et Mercure chez les Latins) est le dieu des voyageurs, des commerçants, des voleurs aussi.
Mercure est la planète du système solaire la plus proche du Soleil (et comme vous le savez, ensuite viennent Vénus et La Terre). Sa température se situe de -180°C la nuit à 400°C.
Mercure est à 57,9 millions de km du Soleil, la Terre à 149,6 millions de km du Soleil.
Le diamètre équatorial de Mercure : 4 878 km ; celui de la Terre est de 12 756 km. Le diamètre de Mercure est sensiblement 3 fois plus petit que celui de la Terre, ce qui signifie que son volume est environ le 1/27 de celui de la Terre. Cependant la masse de Mercure est sensiblement égale aux 5/100 de celle de la Terre !!
(Les renseignements chiffrés que nous donnons sont extraits d'un magnifique ouvrage que nous avons trouvé dans la bibliothèque de votre école : Editeur, Odile Jacob. Auteur André Brahic Titre : Enfants du Soleil. Publié en 1999)
Le mercure ou hydrargyrum ou hydrargyre (ce qui nous donne son actuel symbole Hg utilisé en chimie) ou encore le vif-argent (nom donné à cause de son éclat) est le seul métal liquide à la température ordinaire. Solide dès que l'on atteint la température de -39°C et se vaporise à 357°C. (Liquide à de fortes températures, on comprend aisément qu'il soit utilisé dans les thermomètres ; et ceci s'ajoute au fait qu'il ne mouille pas le verre)
Les Latins le nomment Argentum vivum . . Hydrargyrum nous provient des Grecs et les alchimistes le nommeront aussi aquamétallorum. Peut être sa propriété de s'emparer avidement des métaux pour créer des amalgames lui a-t-elle valu ensuite de s'appeler Mercure, dieu des voleurs !
Le mercure se trouve tant à l'état pur en petite quantité, que surtout sous la forme de sulfure par exemple en Carniole (Italie), à Almaden en Andalousie (Espagne), mais aussi au Mexique, au Pérou,.. et sa production mondiale ne dépasse pas les 9 000 tonnes.
Il forme des amalgames avec de nombreux métaux, or, argent, cuivre … et vous comprendrez mieux pourquoi le professeur de physique qui manipule ses tubes à essai au dessus d'une cuve à mercure… ôte toute alliance ou autre bijou !
Notons enfin que les vapeurs de mercure sont nocives.
|
E0403
|
SUITE DE 2004 NOMBRES.
Cette suite se compose de nombres de 1 chiffre, de nombres de 2 chiffres, de 3 chiffres et de 4 chiffres.
Nombres de 1 chiffre : nous en avons 10 soit 10 chiffres.
N
ombres de 2 chiffres : nous en avons 90 soit 180 chiffres.
Nombres de 3 chiffres : nous en avons 900 soit 2 700 chiffres.
Nombres de 4 chiffres : nous en avons un millier augmenté de 5 ; c'est dire 4 x 1 005 qui est le nombre 4 020.
Et la réponse à ce problème est donc 6 910.
|
| PC0401 |
LES CODES DE CLELIE.
Un code se compose de 4 symboles : 3 chiffres et une lettre.
Il y a 4 cas à considérer selon la position dans le code de la lettre.
1er cas : Le code commence par une lettre (ex : D852)
Il y a 26 choix possibles pour la lettre, puis 10 choix possibles pour le 1er chiffre, puis 10 choix
possibles pour le 2ème chiffre, puis encore 10 choix possibles pour le 3ème chiffre, on obtient donc le
produit suivant : 26×10×10×10 = 26 000
2ème cas : Le 2ème symbole du code est une lettre, alors par la même démarche on obtient encore
26 000 choix.
De même pour les deux derniers cas ; et finalement, le calcul à effectuer était le suivant :
4×26×10×10×10 soit 104 000 codes différents.
|
| PC0402 |
SUR UNE DROITE.
 Il n’y a aucune difficulté à qui sait bien compter et bien regarder !!! Il n’y a aucune difficulté à qui sait bien compter et bien regarder !!!
Nombre de carrés d’aire 1 : 34
Nombre de carrés d’aire 4 : 20
Nombre de carrés d’aire 9 : 14
Nombre de carrés d’aire 16 : 10
Nombre de carrés d’aire 25 : 6
Ce qui nous donne un total de 84 (et un certificat de bonne vision pour ceux qui ont trouvé la bonne réponse).
|
| PC0403 |
Pour distribuer les 325 baramcars, on peut procéder de façon empirique et faire la distribution dans un tableau :
N1 |
N2 |
N3 |
N4 |
N5 |
N6 |
N7 |
Total cumulé par ligne |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
28 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
105 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
231 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
406 c'est 81 de trop |
46 |
50 |
54 |
58 |
36 |
39 |
42 |
Total pour chaque nain |
231+22 = 253
253+23 = 276
276+24 = 300
300+25 = 325 elle a donc donné le dernier baramcar à N4 et c’est lui qui en a reçu le plus !
Les trois derniers nains N5, N6 et N7 ont raté la dernière distribution et parmi eux, c’est N5 qui en a
toujours reçu le moins. C’est donc lui qui en a reçu le moins.
Plus rapide mais…
On remarquera qu’au premier tour Blanche-Neige a distribué 1+2+3+4+5+6+7=28 baramcars et qu’au prochain tour chaque nain en recevra 7 de plus, soit 49 baramcars supplémentaires à distribuer par Blanche-Neige. De même pour le tour suivant.
On obtient donc cette formule dans laquelle t désigne le nombre de tours :
Nombre de baramcars distribués au 1er tour = T1 = 28
Nombre de baramcars distribués au 2ème tour = T2 = 28 + 28 + 49 = 2×28 + 49
Nombre de baramcars distribués au 3ème tour = T3 = 28 + T2 + 2×49 = 3×28 + 3×49
Nombre de baramcars distribués au nème tour = Tn = n×28 + n×49
Dans ce problème il faut donc résoudre d’abord
Tn ≤ 325 soit n×28 + n×49 ≤ 325
n×28 + n×49 ≤ 325
n×77 ≤ 325 d’où n = 4
T3 = 3×28 + 3×49 = 84 + 147 = 231
Et 325 = 231 + 22 + 23 + 24 + 25 alors c’est le nain N4 qui est servi le dernier.
|
| GC0401 |
LA CARTE BANCAIRE DE MME CEPLUHOUT.
Appelons m le chiffre des milliers, c le chiffre des centaines, d le chiffre des dizaines et u le chiffre des unités, ainsi le code cherché est mcdu .
Il suffit alors de lire l’énoncé et de mettre en équation toutes les réactions du chien :
m+c+d+u = 22
m = 3×u
c = 4×d
On en déduit alors facilement que 5×d + 4×u = 22 ; pour cela un seul essai est concluant : u = 3 et d = 2, ce qui nous mène à m=9 et c=8.
Le code est donc 9823.
|
| GC0402 |
JEAN CLAUDE ET ARNAUD.
Les deux premières affirmations de Jean Claude, citoyen du siècle écoulé sont :
- mon age à la fin du siècle est un carré (je le note XY, nombre de 2 chiffres avec éventuellement X = 0 ; nombreuses réponses telles 01, 04, 09, 16, … 81)
- mon année de naissance (étêtée) est aussi un carré et je la note ZT et nous avons donc les mêmes nombreux choix que précédemment).
La somme de ces deux nombres carrés XY et ZT vaut 100.
JC est donc né en 1936 et a eu 64 ans à la fin de siècle ou est né en 1964 et a eu 36 ans en l’an 2000.
Levons cette ambiguïté.
Troisième affirmation de Jean Claude .Arnaud est né en 19UV (postérieure à 1936). A la fin du siècle (an 2000), Arnaud a vécu 100 – UV années.
A la naissance d’Arnaud, Jean Claude a ZT – 36 ans et ce nombre, c’est aussi 100 – ZT. Un calcul
simple donne ZT = 68. Arnaud est né en 1968.
Et tout ceci colle bien. Arnaud né en 68 (Années de célèbres événements, bien entendu celle de la
naissance d’Arnaud aussi). Il a 32 ans en 2000. Jean Claude né en 36, avait 32 ans à la naissance de
son fils et 64 ans à la fin du siècle.
Le problème est fini. Vous avez la réponse: 68.
Les précisions suivantes sont peut être données pour vous amuser un peu.
Oui, 1936 est un carré; 44×44 = 1936 et vous contrôlerez ou démontrerez que c’est la seule année du
XXème siècle dont le millésime est un carré.
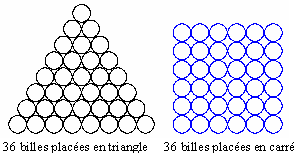 Quant à 36, il est triangulaire et carré. Quant à 36, il est triangulaire et carré.
36 = 6×6 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8.
|
| GC0403 |
FAMILLE NOMBREUSE.
Si f désigne le nombre de filles de cette famille et g le nombre de garçons, l’énoncé nous indique que g = f-1 et que f = 3×(g-1) selon que l’on se place du point de vue d’une fille ou d’un garçon ! car la fille ne se compte pas lorsqu’elle parle de ses sœurs et le garçon ne se compte pas lorsqu’il parle de ses frères.
Ainsi f = 3g – 3 = 3(f-1) – 3 = 3f – 6 d’où 2f = 6 et donc f =3, on a alors g = 3-1 = 2.
Cette famille compte bien 2 garçons et 3 filles.
Prolongement : On a ici résolu algébriquement un système de deux équations à deux inconnues.
On peut aussi résoudre graphiquement ce système à l’aide de deux droites.
La première d’équation y = x-1 et la deuxième d’équation y = 1/3x + 1.
On trace ces deux droites et le point d’intersection est (3 ; 2).
|
| GC0404 |
EN BALLON.
La petite aventure arithmétique (peut être inventée) que nous vous avons proposée se situe bien dans le décor d’une EXTRAORDINAIRE AVENTURE, elle bien réelle, réalisée par le Suisse Bertrand Piccard et le citoyen britannique Brian Jones à la fin du XXème siècle. Nous vous avons fourni les références du livre écrit par les acteurs de l’exploit et je peux supposer et espérer qu’actuellement, vous l’avez lu. Si ce n’était pas le cas, devinez ce qui vous reste à faire !
J’ai certes perdu l’habitude de parler en anciens francs et en Francs pour parler en euros. Mais je n’ai pas encore perdu l’habitude de dire que l’eau gèle à 0° et qu’elle se transforme en vapeur à 100° (je veux parler de l’eau à l’état liquide dans les conditions habituelles dans lesquelles je vis journellement).
Oui, je repère la température sur une échelle dite échelle Celsius ou échelle centigrade sur laquelle conventionnellement la température de fusion de la glace est notée 0°C, et celle de l’ébullition de l’eau par 100°C (C pour Celsius). Bertrand Piccard qui est citoyen suisse, également.
Mais ceci n’est pas toujours le cas pour Brian Jones, citoyen de sa gracieuse majesté La Reine d’Angleterre qui, comme nombre de ses concitoyens, utilise encore une autre échelle qui n’est plus officielle, l’échelle Fahrenheit. Dans cette échelle, la glace fond à 32° que l’on note 32°F et l’eau bout à 212°F.
La distance 100 que nous lisons sur l’échelle Celsius entre les températures de réalisation de deux phénomènes physiques (transformations de l’eau de l’état liquide en glace et de l’état liquide en vapeur) correspond à une distance de 180 sur l’échelle Fahrenheit. Une élévation de température de 1°C de ce côté de la Manche équivaut à une élévation de 1,8 °F de l’autre côté !
Vous pouvez donc facilement convertir une température t C donnée dans notre échelle par la même température donnée sur l’échelle t F.
X°C = (1, 8 X + 32)° F.
X °F= (( X – 32 ) : 1,8)°C.
(Je vous engage à contrôler que les renseignements fournis dans le texte du concours ont bien été calculés). Et si nous revenions à ce dernier !
L’énoncé fournit 4 couples de données (2 de ces couples sont donnés en trop et permettent de vérifier vos calculs).
X en Celsius |
-2 |
-20 |
0 |
100 |
Y en Fahrenheit |
28,4 |
- 4 |
32 |
212 |
Méthode par tâtonnement : il n'y a guère de commentaire à faire.
Méthode graphique : Tracez les deux droites Y = 1,8 X + 32 et Y = X. Un travail sérieux vous permet de lire les coordonnées du point de concours de ces droites qui sont – 40 et – 40.
Méthode algébrique : En appelant X et Y les températures (encore une habitude de nommer les inconnues), il suffit de résoudre un système de deux équations du premier degré à deux inconnues :
Y = 1,8 X + 32 et Y = X à X = 1,8 X + 32 à - 32 = 0,8 X et X = - 40
Remarque : Il est implicite que les écarts de température sur les deux échelles sont proportionnels.
Nota
Bertrand Piccard né le 1 er mars 1958.
Brian Jones né le 27 mars 1947.
Le Tour du monde en 20 jours : Départ le 1er mars 1999 de Château-d’Oex (Suisse). Arrivée le 21 mars dans le désert égyptien soit après un voyage de 19 jours, 21 heures et 47 secondes ; Le Tour du monde en 20 jours. Livre édité par Bernard Laffont. Auteurs : Bertrand Piccard et Brian Jones. Publié en 1999.
Celsius Anders (1701-1744) Astronome et Physicien suédois. L’échelle de température qu’il propose admet le 0 pour l’ébullition de l’eau et 100 pour la température de la glace fondante.
Fahrenheit Daniel (1686-1736) Physicien allemand à qui l’on doit l’invention de l’aréomètre et de l’échelle des températures décrite dans cet article.
|



