Rappelons tout d’abord les règles du minisudoku, moins connues que celles de son glorieux aîné. L’exemple qui suit (ainsi que tous ceux qui illustrent le présent article) a été simplement tiré d’un journal gratuit :

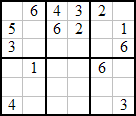
La grille doit être complété de manière que chaque colonne, chaque rangée, et chaque rectangle en gras comporte les chiffres de 1 à 6.

Prenez si vous le voulez quelques minutes pour résoudre cette grille et pour observer un instant votre solution, ainsi que les pièces de votre jeu de dominos :

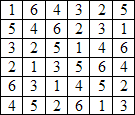
Peut-être l’avez-vous deviné ? Le défi des sudominos consiste à disposer vos dominos en respectant la condition suivante :

Règle des sudominos : Les dominos doivent être placés sur la grille de façon que les valeurs qu’ils portent coïncident à avec celles indiquées par les cases.

Votre jeu traditionnel compte 28 dominos, mais vous n’aurez à utiliser ni les « blancs », ni les doubles : restent 15 dominos simples, occupant un total de 2 × 15 = 30 cases. Si donc vous parvenez à placer vos 15 dominos sur ce plateau, il restera nécessairement 6 cases inoccupées, c’est-à-dire précisément le nombre de cases constituant une colonne, rangée, ou l’un des rectangle en gras qu’il vous fallait compléter précédemment à l’aide des chiffres de 1 à 6… Il est donc tentant de s’imposer comme motif pour les six cases exclues une disposition selon une rangée, une colonne, ou l’un des six rectangles gras de la grille de départ: Voyons comment ceci s’applique à notre exemple :

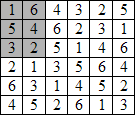
Nous nous interdisons ici de placer nos dominos sur les six cases du coin supérieur gauche (en gris sur la figure)… Il n’y a alors qu’un emplacement pour le domino 3-6:

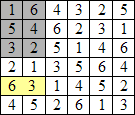
Les placements des dominos 4-5 et 2-1 sont forcés…

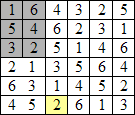
Il s’ensuit que la case 2 située à droite du domino 4-5 ne peut plus être associée qu’au 6…

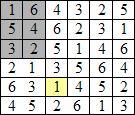
Supposons maintenant que le 1 situé au dessus de cette case soit associée au 3 le surplombant. Alors le 4 à sa droite serait nécessairement associé à un 5, ce qui est interdit puisque le 5-4 a déjà été placé. En conséquence, l’emplacement du 1-4 est forcé.

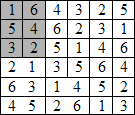
En raisonnant de façon similaire, on place successivement les dominos 2-4, 1-3, 5-6, 5-2, 1-6, etc. et on aboutit à la répartition finale :

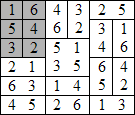
Dans cette configuration le carré central peut-être indifféremment partagé par une ligne horizontale ou verticale afin de faire apparaître deux solutions distinctes. Il est doublement remarquable que les règles du sudoku semblent favoriser les placements de nos dominos, et que les types de raisonnements qui conduisent à résoudre ce dernier problème soient si souvent similaires à ceux qui permettaient de venir à bout du premier ! Evidemment, certaines grilles n’admettent aucune solution, par exemple :

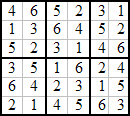
Question 1 : Voyez-vous pourquoi cette grille est insoluble ? Toutefois, mon expérience me pousse à penser que dans la plupart des cas, les minisudokus devraient pouvoir être recyclés en minisudominos, la difficulté résidant principalement dans le choix judicieux des six cases à exclure…

Sudominos 9×9

Nous n’avons pour l’instant envisagé que les minisudokus. La transposition à une grille standard de sudoku est évidente. On trouve dans des magasins spécialisés ou sur internet des jeux de 55 dominos aux valeurs allant de 0 à 9, mais on peut également résoudre de telles grilles à l’aide d’un crayon, de papier et … d’une forte dose de patience ! En ôtant les doubles et les blancs, il vous reste 55- 10- 9 = 36 dominos qui occuperont donc 2 ×36 = 72 cases, soit encore exactement le total des cases d’une grille de sudoku amputée d’une rangée, d’une colonne ou d’un carré gras ! On peut donc encore une fois tenter de résoudre de telles grilles en excluant une ligne, une colonne, ou un carré de notre grille.

Question 2 : s’agit-il d’un résultat général, ou d’une simple coïncidence ? Plus précisément, la surface totale d’un jeu complet de dominos sans doubles ni blancs, est-elle toujours égale à celle d’un rectangle comptant une rangée de moins que de colonnes ?

Les grilles de 81 cases sont en général beaucoup, beaucoup plus difficiles que celles de 36 cases , ce qui rend leur résolution d’autant plus gratifiante. En partant de grilles piochées au hasard dans les journaux, je pense qu’il doit être rare de parvenir à les résoudre en répartissant les cases inoccupées selon un rectangle de 9 cases ; un tel exemple figure néanmoins à la fin du présent article.

Etant donné que les grilles suscitées ne sont pas conçues pour le sudomino, la découverte d’une solution procure des satisfactions multiples allant de la surprise de son existence au plaisir d’avoir triomphé d’un casse-tête redoutable, en passant par le sentiment d’accomplissement qu’accompagne la mise au point de stratégies originales de résolution…Certains préfèreront cependant s’attaquer à des grilles de sudomino dont l’existence d’une solution est garantie. Sous sa forme classique, une telle grille se présentera comme un sudoku dont neuf cases auront été coloriées : celles qui devront rester inoccupées après complétion et placement des dominos.

Par exemple :

Exemple d’énoncé de sudomino:

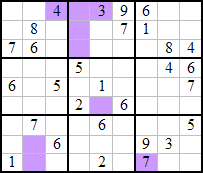
Solution :

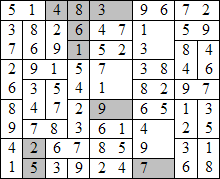
Exemple d’énoncé incorrect de sudomino:

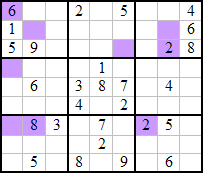
Question 3 : une erreur s’est à coup sûr glissée dans cette grille de sudominos. Voyez-vous pourquoi ?

Dans votre quête, n’oubliez pas de vous assurer de l’unicité de la solution de votre sudoku : certains créateurs peu scrupuleux s’affranchissent allègrement de cette convention (pourtant précieuse à la résolution) . Une fois tous vos dominos en place, relevez les emplacements des cases inoccupées et proposez ensuite votre grille de sudomino à quelque adepte de ce genre de casse-tête… moi, par exemple ! Le domaine des sudominos reste largement à explorer… Peut-être découvrirez-vous des grilles de sudominos particulièrement belles, respectant la contrainte d’une formation en bande ou en carré des neuf cases inoccupées ou toute autre configuration harmonieuse ? On peut par exemple privilégier des dispositions des neuf cases coloriées présentant des propriétés de symétrie, ou dessinant une forme facilement identifiable, ou choisies dans l’ensemble des chiffres fournis par l’énoncé du sudoku, etc.… Voilà en tous cas de nouveaux défis en cascade pour amateurs de casse-tête, informaticiens ou mathématiciens en herbe…

A vous de jouer !

Minisudominos :

Niveau débutant : Le minisudoku a déjà été résolu, il ne vous reste plus qu’à disposer vos 15 dominos à l’intérieur des cases non coloriées.

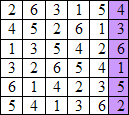
Niveau moyen : Cette fois, c’est à vous de résoudre ce minisudoku, puis de disposer vos 15 dominos sur les cases non coloriées.

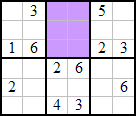
Prolongement : pouvez-vous, pour chacun des problèmes précédents, trouver d’autres choix de rectangles de six cases inoccupées permettant la résolution de la grille ?

Sudominos « classiques »

Niveau difficile : Le sudoku a déjà été résolu, il ne vous reste plus qu’à disposer vos 36 dominos à l’intérieur des cases non coloriées.

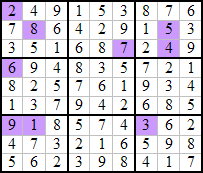
Niveau expert :

Résolvez ce sudoku (dificile), puis disposez vos 36 dominos sur les cases non coloriées de votre solution.

Même défi, mais cette fois avec un sudoku de niveau moyen.

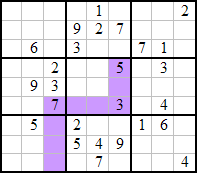
Solutions au prochain numéro…

Marc Genevey

 

Réponses aux questions de ce numéro :

Q1 : il est impossible de placer le domino 3-4. Q2 : le résultat est général ! Le nombre de dominos d’un jeu à n valeurs ( par exemple allant de 0 à n-1) vaut n(n+1)/2. Enlever les doubles ramène ce nombre à n(n+1)/2 – n = (n² +n -2n)/2 = (n²-n)/2 . Comme chaque domino occupe deux cases, la surface totale d’un tel jeu de dominos vaut n²-n, c’est-à-dire exactement celle d’un carré de côté n amputé d’une colonne. Q3 : Les chiffres de 1 à 9 sont équitablement répartis, tant sur les dominos que sur la grille. Les cases inoccupées doivent donc obligatoirement porter les valeurs de 1 à 9. Ici la valeur 2 figure deux fois parmi les cases inoccupées : il y a donc une erreur.