Au pays des mathématiques, on annonça un jour un concours parmi les quadrilatères pour choisir celui ayant la plus grande surface. Pour que la compétition soit équitable, les juges décidèrent qu'on ne comparerait que des quadrilatères ayant un périmètre fixé une fois pour toutes.

L'annonce ( sur le Web local ) précisait qu'on n'examinerait que des " quadrilatères isopérimétriques " pour trouver celui ayant la plus grande surface. Les savants reconnurent les mots grecs ( les mathématiques doivent beaucoup à la Grèce ) : iso pour égal, péri pour " autour ", l'idée de périmètre, et metron la mesure. Ils surent aussi que le périmètre vaut la somme des longueurs des côtés. L'annonce du concours était formulée comme un problème mathématique : Parmi tous les quadrilatères de périmètre donné, trouver celui de plus grande surface .

Tous les quadrilatères se mirent sur leur trente-et-un, espérant gagner le concours. Certains avaient un angle rentrant, d'autres étaient des parallélogrammes ou des rectangles, et la plupart avaient des côtés de longueurs distinctes. On remarquait aussi le carré parmi les prétendants. Le jour du concours un juge appela tous les quadrilatères de périmètre fixé.

Le premier qui arriva (figure 1) avait un angle rentrant, il s'appelait M. Concave et quand il annonça que c'était lui qui avait la plus grande surface, le juge dit en souriant : " ça ne peut être le cas, regardez, je peux par réflexion vous transformer (et il dessina la figure 2) pour obtenir, en ôtant l'angle rentrant, un quadrilatère de même périmètre mais avec une plus grande surface ".

Et du coup, le juge demanda à tous les quadrilatères qui n'étaient pas convexes, autrement dit qui ne contenaient pas leurs diagonales, d'abandonner la compétition, puisqu'ils n'avaient aucune chance de l'emporter.

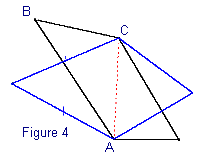
Il ne restait déjà plus dans la compétition que les quadrilatères convexes ayant tous le même périmètre P. Alors M. Inégal (figure 3) se présenta : il avait deux côtés qui se suivaient (adjacents) de longueur différente et il annonça qu'il avait la plus grande surface. Le juge jeta rapidement un coup d'œil , il le divisa le long d'une diagonale, et il lui dit : " Non, M.Inégal, vous n'avez pas la plus grande surface car, en remplaçant les deux côtés par des côtés égaux comme ceci (figure 4), je peux vous transformer en un quadrilatère de plus grande surface, tout en gardant le même périmètre ". M.Inégal voulut protester mais le juge lui fit remarquer qu'un triangle comme ABC dont les côtés ont une somme constante est de surface maximale quand il est isocèle.

Question 1. Pouvez-vous le montrer ?

M.Inégal rentra chez lui réfléchir à la question mais finalement il fut convaincu. Après cet incident, le juge conclut qu'il suffisait dorénavant de considérer seulement les quadrilatères tels qu'une diagonale les divise en deux triangles isocèles.

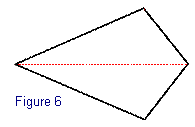
Monsieur Cerfvolant se mit en avant : il répondait à la condition mais il avait deux côtés de longueur différente (figure 5) et il déclara : " Maintenant que tous les autres ont été éliminés, c'est certainement moi le gagnant ! ". Le juge regarda de près M.Cerfvolant et soudain s'exclama " Aha ! "…et le coupa par l'autre diagonale (figure 6).

Question 2. Comprenez-vous la réflexion du juge ?

" Oui, dit le juge, vous devez avoir tous les côtés égaux (autrement dit être un losange) ". Cette fois-ci il ne restait plus dans la compétition que des losanges. Monsieur Losange se lève alors et annonce : " Il est facile de calculer ma surface ; comme les quatre côtés sont égaux, ma surface est le produit du côté par la hauteur ".

Question 3. Pourquoi ?

" C'est exact, dit le juge, donc pouvez-vous me dire qui a gagné le concours ? ". M.Losange répondit : " Comme je dois avoir la hauteur la plus haute possible, il faut que j'ai des angles droits ". " Autrement dit, répliqua le juge, c'est le carré qui a gagné ! ". Et il annonça au haut-parleur le résultat du concours : parmi les quadrilatères ayant un périmètre donné, c'est le carré qui a la plus grande surface.

La compétition étant terminée, les quadrilatères revinrent chez eux, déçus (sauf le carré). Le problème isopérimétrique pour les quadrilatères venait d'être réglé. Le carré était le gagnant, le fait (au pays des mathématiques on dit un théorème) était clairement établi, par les explications du juge ( sa démonstration).

Vagn Lundsgaard Hansen (V.L.Hansen@mat.dtu.dk)
Auteur de Geometry in Nature (A.K.Peters, 1993)
et Shadows of the Circle (World Scientific, 1998)
Le présent article est inspiré d'un article du même auteur : " I am the greatest "
(Mathematics in school, vol.25, n°4, 1996, Grande-Bretagne).